numpy-thonic run length compression …
I’ve been tinkering with my
cam_board
script. This little program can turn a web cam into a white / black
board. I found it handy in these rough, socially isolated, disease
ridden times. The de-noising feature of the script is particularly
useful when recording the “blackboard” for students because it greatly
reduces the video file sizes. I was wondering if it would be possible to
have a compression algorithm built into the script. Ideally, to reduce
compression time, the compression procedure would rely heavily on the
fast methods of the numpy library. This post describes the
resulting algorithm. This description is also part of an assignment
where I ask students to implement the same algorithm without
numpy and compare compression times. The script and sample
image can be downloaded from
here.
The script begins with two import statements in [compress.py line: 9] :
import numpy
import matplotlib.pyplot as pltLoading the binary image
In our example we will be working with a 720 by 1280 image. The
individual pixels in this image will contain one of two values : 0 , 1.
This means that 921600 bits or 115200 bytes are used to represent the
image. The image data is stored in image.npy in a special
format designed to store numpy arrays. This file was
created using the numpy.packbits function and you can
verify that it is almost exactly 115200 bytes long.
The file is loaded and stored in variable a in
[compress.py line: 67] :
a = numpy.load("image.npy")and next it is unpacked in [compress.py line: 70] :
a = numpy.unpackbits(a)Information about a is printed to the standard output in
[compress.py line: 74] :
print("a.shape : " , a.shape)
print("a.dtype : " , a.dtype)The first print statement will result in:
a.shape : (921600,)which means that we are dealing with a one dimensional array of size 921600. This is used in [compress.py line: 79] :
length = a.shape[0:1]to assign the length of a to a variable. The second
print statement will result in:
a.dtype : uint8from which we can gather that all values in this one dimensional array are unsigned 8-bit integers.
The unpacked array of unsigned 8-bit integers can be saved to a file. This is done in [compress.py line: 83] :
numpy.save("image_unpacked" , a)and the resulting file image_unpacked.npy contains
921728 bytes. This is almost eight times more then
image.npy.
Compression method
The idea behind the compression method is simple. More formally the algorithm that will be implemented belongs to a family of run time compression algorithms.
Since the data we are working with is just a string of 0, 1 :
0 1 1 1 1 1 1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 1 ...it will be represented by the lengths of sequances of ones and zeros that appear the sequence:
1 8 1 3 8 ...This information together with the value of the first element of the sequence :
0can be used to reconstruct the original image.
The value of the first element of a is assigned to a
variable in [compress.py line: 138] :
first = a[0:1]Notice that the variable first points to a
numpy array and not a single value. This array was created
by taking a segment of a (a[0:1]), that is
elements with indexes greater or equal to 0 and less then 1. This means
that first is a one dimensional array with one element -
the first value in a. The choice to use an array with a
single element instead of a single value will be useful later when
first will be concatenated with other arrays.
In order to obtain a lengths of sequences for the compression algorithm first a list of indexes with non zero elements (ones) is created and assigned to a variable in [compress.py line: 142] :
nonzero = numpy.nonzero(a)[0]The next lines [compress.py line: 146] :
start = numpy.nonzero((numpy.roll(nonzero,1) + 1) - nonzero)[0]
end = numpy.nonzero((numpy.roll(nonzero,-1) - 1) - nonzero)[0]
ones = end - start + 1result in the variable ones containing a list of lenths
of 1 , 1 , 1 , ... sequences in a. This code
uses a combination of numpy functions. The reader is
encouraged to try this code out in ipython and read the
documentation on these routines. The next lines of code [compress.py
line: 152] :
ai = 1 - a
nonzero = numpy.nonzero(ai)[0]
start = numpy.nonzero((numpy.roll(nonzero,1) + 1) - nonzero)[0]
end = numpy.nonzero((numpy.roll(nonzero,-1) - 1) - nonzero)[0]
zeros = end - start + 1result in the variable zeros containing a list of
lengths of 0 , 0 , 0 , ... sequences in a.
Compressed data
All the data necessary to reconstruct the original image is concatenated in [compress.py line: 175] :
data = numpy.concatenate(
(
length ,
first ,
zeros.shape[0:1] ,
zeros ,
ones.shape[0:1] ,
ones
))In order to firther save space, this array is rewritten using unigned 32-bit integers in [compress.py line: 187] :
data = data.astype("uint32")Finally the data is saved to image_compressed.npy in
[compress.py line: 198] :
numpy.save("image_compressed" , data)Notice that the size of this file is only 20892 bytes.
Reconstructing the original image
Now it is time to to check if it is possible to reconstruct the
original image from image_compressed.npy. In the first step
this file is loaded from disk [compress.py line: 212] :
comp = numpy.load("image_compressed.npy")Next in [compress.py line: 232] :
l = comp[0]
f = comp[1]
zs = comp[2]
z = comp[3 : 3 + zs]
os = comp[3 + zs]
o = comp[3 + zs + 1:]the
a0 0 0 ... sequence lengths0 0 0 ... sequence lengths1 1 1 ... sequence lengths1 1 1 ... sequence lengthsare assigned to variables.
Next in [compress.py line: 251] :
rif = numpy.empty(zs + os , dtype = z.dtype)
val = numpy.empty(zs + os , dtype = z.dtype)
if(first == 0):
rif[0::2] = z
rif[1::2] = o
val[0::2] = 0
val[1::2] = 1
else:
rif[0::2] = o
rif[1::2] = z
val[0::2] = 1
val[1::2] = 0two, initialy empty, numpy arrays are created.
rif will contain interwoven 0 0 0 ... and
1 1 1 ... sequence lengths and val will
contain the values (0 or 1) associated with the corresponding sequence
length. Note the [0::2] and [1::2] operators
used for achieve this. They allow assigning values to every second
element of a numpy array starting with the first (index 0)
or second (index 1) element.
The original array is reconstructed in [compress.py line: 278] :
reconstruct = numpy.repeat(val , rif)
reconstruct = reconstruct.astype("uint8")and tested against the original array a in [compress.py
line: 283] :
print("test against original : " ,
numpy.array_equal(a , reconstruct))using the numpy.array_equal function.
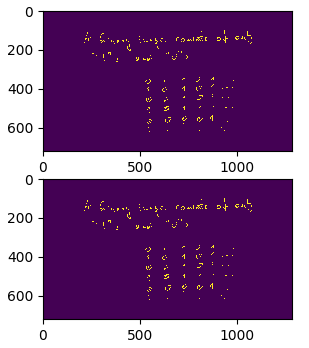
Drawing the images
In [compress.py line: 308] :
fig , axs = plt.subplots(2)a plot containing two subplots is created. One subplot will contain the original image and the other one will contain the reconstructed image. In order to draw the images, the one dimensional arrays have to be reshaped first in: [compress.py line: 312] :
img_compressed = a.reshape((720 , 1280))
img_reconstruct = reconstruct.reshape((720 , 1280))Finally in [compress.py line: 317] :
axs[0].imshow(img_compressed)
axs[1].imshow(img_reconstruct)
plt.show()the arrays are plotted and shown.

2021-01-22 EDIT: minor corrections