Zestawy zadań

Zawartość:
- Ocenianie
- Zestaw 1
- Zestaw 2
- Zestaw 3
- Zestaw 4
- Zestaw 5
- Zestaw 6
- Zestaw 7
- Zestaw 8
- Zestaw 9
- Zestaw 10
- Zestaw 11
Ocenianie
- Ćwiczenia można oddawać na każdych zajęciach, wystarczy zademonstrować działanie programu oraz króciutko o nim opowiedzieć.
- Ćwiczenia z zestawu przypadającego na dane zajęcia można oddawać do
końca semestru ale …
- … jeżeli pod koniec semestru braknie czasu na zajęciach aby zadanie oddać to nie zostanie ono zalicone
- W związku z tym proszę nie zwlekać z oddawaniem zadań.
- Ocena z zadań będzie wystawiana na podstawie całkowitej ilości punktów uzyskanych z rozwiązania ćwiczeń.
Zestaw 1
Tworzenie skryptu, metoda 1 (prostsza):
po uruchomieniu programu mathematica należy w menu wybrać: File - New - Package/Script - Wolfram Language Script
w nowym okienku mozna wpisać treść programu
po zakończeniu edycji zapisujemy skrypt i zamykamy okienko (to ważne, Mathematica korzysta z mechanizmu uniemożliwiającego jednoczesną edycję oraz wykonanie skryptu)
w terminalu (pod linuxem tak, pod windows tak) nawigujemy do katalogu gdzie znajduje się skrypt i uruchamiamy komendą (pod linux, pod windows jest trochę inaczej - proszę samodzielnie po eksperymentować):
... $ ./nazwa_skryptu.wls
Tworzenie skryptu, metoda 2 (linux ale bardziej uniwersalna w tym systemie):
otwieramy ulubiony edytor tekstu
wpisujemy do pliku program
w pierwszej linijce (tzw linijka “hash bang!”, musi być zawsze pierwsza, nad nią nie mogą się znajdować puste linie) dodatkowo dodajemy:
#!/usr/bin/env wolframscriptlinijka ta informuje system operacyjny, który program powinien być wykorzystany do zinterpretowaniu programu zawartego w skrypcie
alternatywnie można zamieścić bezpośrednią ścieżkę do programu, na moim systemie wygląda ona następująco:
#!/usr/local/Wolfram/Mathematica/12.1/Executables/wolframscriptteraz wystarczy nawigować w terminalu do katalogu zawierającego skrypt, zezwolilć aby nasz skrypt był wykonany:
... $ chmod +x nazwa_skryptu… i go wykonać:
... $ ./nazwa_skryptuskrype można również wykonać z argumentami, np:
... $ ./silnia 5
Kilka przykładowych skryptów:
Kilka chaotycznych notebooków z zajęć (polecam zaglądnąć najpierw do materiałów profesora Jacka Golaka):
Proszę zainstalować i uruchomić program Mathematica.
Korzystająć z notebooka proszę zaimplementować ciąg liczb Fibonacciego \(0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21, \ldots\).
Korzystając z implementacji z zadania B proszę stworzyć uruchamialny skrypt. Skrypt powinien z linii poleceń pobierać pojedyńczy argument, liczbe wyrazów w ciągu Fibonacciego. Państwa program powinien następnie wypisywać na ekranie odpowiednią liczbę początkowych wyrazów tego ciągu.
Zestaw 2
W razie kłopotów:
- Evaluation - Quit Kernel - Local resetuje jądro mathematici. Wszystkie definicje zmiennych, funkcji, … zostaną usunięte.
- Evaluation - Abort Evaluation przerywa aktualnie wykonywane zadanie
Ostatnie twierdzenie Fermata:
Szablony, wzrce: Help - Wolfram Documentation i w okienku:
- guide/Patterns
- tutorial/Patterns
Chaotyczny notebook z zadań (lepiej przyjrzeć się wykładowi profesora):
Zadanie A:
- proszę dokładnie :-) przyjrzeć się wszystkim rozdziałom
dokumentacji
FullSimplifyLiczenie objetości bąbelków (proszę zajrzeć równiez do drugiego wykładu profesora):
Notebooki z zajęć 13 X, aby uruchomić wszystkie komórki wystarczy w menu wybrać Evaluate - Evaluate Notebook:
Proszę, z wykorzystaniem funkcji
FullSimplifysprawdzić czy istnieją liczby całkowite \(x\) , \(y\) , \(z\) oraz \(n\), które spełniają:
- \(x^n + y^n = z^n\)
- \(n > 2\)
- \(x y z \ne 0\) (żadna z tych liczb nie jest równa 0)
Proszę skonstruować krótki dowód wyniku z zadania A. Zeskanowane wyprowadzienie można mi wysłać pocztą elektroniczną.
Proszę z wykorzystaniem funkcji
Ifzaimplementować funkcję \(f(x , y)\), która przyjmuje wartość \(1\) gdy punkt \((x , y)\) wpada w dwu-wymiarowy pierścień o zewnętrznym promieniu \(1\) oraz wewnętrznym promieniu \(\frac{1}{2}\) ze środkiem w środku układu współrzędnych. W przeciwnym wypadku funkcja przyjmuje wartość \(0\). Proszę tą funkcję narysować z wykorzystaniem
RegionPlotKorzystając z funkcji:
Integrateproszę policzyć pole pierścienia z zadania C. Wskazówka: Całka \(f(x , y)\) po \(x\) oraz \(y\) w zakresie od \(-1\) do \(1\) zwróci pole koła. Dlaczego?
Ciało o masie \(1\) kg porusza się po trajektorii \(r(t)\) zaimplementowanej jako:
(*t - czas w sekundach*)
(*{x , y} - zwracana pozycja w metrach*)
r[t_] := {Cos[t] , Sin[t]};Proszę policzyć jaka siła musi działać na to ciało jeżeli założymy, że porusza się ono zgodnie z zasadami Newtona. Można w tym celu wykrozystać funkcję:
DProszę skonstruować funkcję, która dla zadanego czasu będzie zwracała graficzną reprezentację ciała oraz działającej na niego siły.
Korzystając z funkcji:
Importoraz
CasesProszę napisać program który:
- pobierze ze strony
plik CSV zawierający dane dotyczące liczby potwierdzonych przypadków
- można skopiować link https://github.com/CSSEGISandData/COVID-19/raw/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv
- wykorzystać go w funkcji
Import - zwróci wykres nowych przypadków dla Polski z ostatnich czterech tygodni
Korzystająć z definicji pochodnej oraz funkcji:
LimitProszę policzyc pochodne \(f'(x)\) następujacych funkcji:
- \(f(x) = ln(x)\)
- \(f(x) = exp(x)\)
- \(f(x) = x^{2}\)
Korzystając z
Manipulateproszę napisać program, który będzie manipulował wykresem funkcji \(f(x) = exp(x) sin(4 x)\). Implementacja powinna pozwalać na wykonanie operacji:
- przesunięcia wykresu funkcji w górę lub dół
- przesunięcia wykresu funkcji w lewo lub prawo
- odbicie funkcji względem osi pionowej
- odbicie funkcji względem osi posiomej
Zestaw 3
- wprowadzenie do liczb
zespolonych
- nie oglądałem tego wykładu do końca ale Grant Sanderson zazwyczaj doskonale tłumaczy, polecam
- chaotyczne notatki
- lepiej zerknąć do wykładu 3Blue1Brown
- … lub Państwa notatek z matematyki
- chaotyczny notebook
- lepiej zerknąć do wykładu 3Blue1Brown
- … lub Państwa notatek z matematyki
- pisanie pakietów
- notebook z 20 X 2022, grupa poranna
- notebook z 20 X 2022, grupa wieczorna
Korzystająć z:
NSolveproszę znaleźć wartści \(x\) dla których zachodzi:
- \(f(x) = 0\), gdzie \(f(x) = \frac{\sin{x^{2}}}{x^{2}}\)
- \(x < 2 \pi\)
- \(x > 0\)
Korzystając z funkcji
Plotoraz opcjonalnych argumentów:
GridLines -> ... ,
PlotStyle -> ... ,
Frame -> ... ,
Axes -> ... ,
FrameLabel -> ...Proszę narysować wykres funkcji \(f(x)\) z zadania A w przedziale o \(0\) do \(2 \pi\). Wykres powinien:
- być narysowany czerwoną linią
- zawierać pionowe linie w miejscach gdzie w A wyliczono \(f(x) = 0\)
- zamiast osi posiadać ramkę
- zawiera opis pionowej oraz poziomej osi na ramce
Proszę wprowadzić definicje dwóch macierzy w postaci zagnieżdżonych list:
\[ A = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right) \]
\[ B = \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \\ \end{array} \right) \]
oraz sprawdzić z wykorzystaniem funkcji
Dotile wynoszą iloczyny macierzy:
- \(A.A\)
- \(B.B\)
- \(\left( a_{1} A + b_{1} B \right).\left( a_{2} A + b_{2} B \right)\)
- \(\left( a_{2} A + b_{2} B \right).\left( a_{1} A + b_{1} B \right)\)
gdzie \(a_{1}\), \(b_{1}\), \(a_{2}\), \(b_{2}\) są liczbami rzeczywistymi. Czy można te wyniki wykorzystać do reprezentacji liczb zespolonych? Dlaczego?
Proszę powtórzyć rachunki z zadania C dla macierzy:
\[ A = \left( \begin{array}{cc} 1 & 0 \\ -1 & 1 \\ \end{array} \right) \]
\[ B = \left( \begin{array}{cc} 1 & 1 \\ 1 & 0 \\ \end{array} \right) \]
Liczenie eksponenty liczby \(x\): \[ e^{x} \] można uogólnić do macierzy z wykorzystaniem rozwinięcia \[ e^{x} = \sum_{k = 0}^{\infty} \frac{x^{k}}{k!} = 1 + x + \frac{1}{2} x^{2} + \frac{1}{6} x^{3} + \ldots \] oraz zastępując mnożenie, mnożeniem macierzowym. W Mathematice eksponentę z macierzy można policzyć wykorzystując:
MatrixExpProszę:
policzyć \(e^{B \phi}\) gdzie \(B\) jest macierzą z zadania C
wykorzystując
Solvezapisać ten wynik w postaci \(a A + b B\) gdzie macierze \(A\), \(B\) są z zadania C natomiast \(a\), \(b\) są nieznanymi liczbami
Jak ten wynik ma się do liczb zespolonych?
Proszę wykorzystać wzorzec:
f[c_][z_] := ...aby zaimplementować funkcję \[ f_{c}(z) = z^{2} + c \]
Następnie, korzystając z wzorca:
k[n_][c_] := ...funkcji:
Nestoraz implementacji funkcji \(f\) proszę zaimplementować funkcję \(k_{n}(c)\) która dla danej liczby zespolonej \(c\) oraz początkowej liczby zespolonej \(z_{0} = 0\) wielokrotnie aplikuje funkcję \(f\):
\[k_{1}(c) = f_{c}(z_{0})\] \[k_{2}(c) = f_{c}(f_{c}(z_{0}))\] \[k_{3}(c) = f_{c}(f_{c}(f_{c}(z_{0})))\] \[\ldots\]
Wykorzystując
RegionPlot
Absproszę narysować funkcję \(1 / |k_{5}(x + i y)|\) gdzie \(-2 < x < 1\) oraz \(-1.5 < y < 1.5\). Co otrzymujemy? Czy można \(1/||\) zastąpić inną funkcją?
Wykorzystując
Limitproszę policzyć granice (WSKAZÓWKA: proszę zajrzeć do dokumentacji ;-) :
- \(\lim_{x \rightarrow 0^{+}} \frac{|x|}{\sin x}\)
- \(\lim_{x \rightarrow 0^{-}} \frac{|x|}{\sin x}\)
oraz narysować wykres funkcji \(\frac{|x|}{\sin x}\).
Proszę wykonać zadanie A biorąc pochodną funkcji \(f(x)\), \(f'(x)\), zamiast \(f(x)\).
Wykorzystując
DiscretePlot
DiscreteLimitproszę narysować wykres funkcji: \[ f(k) = \sin(k \pi / 16) / k \] , gdzie \(k\) jest liczbą całkowitą, oraz znaleźć jej granicę przy \(k \rightarrow \infty\).
Zestaw 4
- slajdy z zajęć 2020/2021
- nagranie z zajęć
- notebook rozwiązujący równanie laplaca
- chaotyczny notebook z zajęć
- chaotyczne notatki
- przykładowy
pakiet
MyFirstPackage.wl- pakiettest.nb- notebook z przykładowym użyciem- uwaga,
MyFirstPackage.wloraztest.nbpowinny być w tym samym katalogu
Korzystając z wyniku zadania E z zestawu trzeciego proszę uzasadnić: \[ exp(i \phi) = cos(\phi) + i sin(\phi) \] gdzie \(\phi\) jest liczbą rzeczywistą.
Proszę potwierdzić tą zależność rozwijając \(exp(i \phi)\) z wykorzystaniem:
ComplexExpandFunkcja ta rozwija dowolne wyrażenie zakładając, że wszystkie występujące w niej niewiadome są rzeczywiste.
Proszę uogólnić zadanie E z zestawu trzeciego i z wykorzystaniem
MatrixExppoliczyć \(e^{x A + y B}\) gdzie \(x, y\) są liczbami rzeczywistymi. Jak ten wynik ma się do liczb zespolonych?
Korzystając z równań Cauchiego-Riemana (bez paniki, objaśnię na zajęciach i podam przykład) oraz
DSolveproszę policzyć funkcję \[ sin(x + i y) \] gdzie \(x , y\) są liczbami rzeczywistymi przy założeniu, że jest ona analityczna (z założenia tego wynika, między innymi, że posiada ona pochodne) i znamy jej wartości dla \(sin(x + i 0) = sin(x)\).
Wynik proszę porównać z rozwinięciem \(sin(x + i y)\) za pomocą
ComplexExpanddla kilku wartości \(x\) oraz \(y\). Dodatkowo z wykorzystaniem
ContourPlotproszę narysować wykres części rzeczywistej oraz urojonej \(sin(x + i y)\).
Zajmiemy się obiektami typu
cn[x , y]gdzie \(x , y\) są liczbami rzeczywistymi. Dla wyrażeń tego typu zdefiniowane są operacje
plus[cn[x1_ , y1_]][cn[x2_ , y2_]] := cn[x1 + x2 , y1 + y2]times[cn[x1_ , y1_]][cn[x2_ , y2_]] := cn[x1 x2 - y1 y2 , x1 y2 + y1 x2]re[cn[x_ , y_]] := xoraz
im[cn[x_ , y_]] := yktóre nazywamy dodawaniem, mnożeniem, braniem części rzeczywistej oraz braniem części urojonej.
Łatwo się domyślić, że obiekty tego typu mogą reprezentować liczby zespolone. Proszę to sprawdzić i zdefiniować funkcję
powerktóra dla liczby całkowitej \(n\) oraz obiektu typu jak wyżej \(z\)
power[n][z]zwraca potęgę \(z^{n}\). Wskazówka: można skorzystać z funkcji
Nestale przypadek podnoszenia do potęgi \(0\) trzeba rozważać osobno.
Wiedząc, że \[ Re(e^{i \phi}) = cos(\phi) \] oraz \[ Im(e^{i \phi}) = sin(\phi) \] proszę policzyć \(cos(1)\) oraz \(sin(1)\) z wykorzystaniem rozwinięcia eksponenty w szereg \[ e^{z} = exp(z) = \sum_{k = 0}^{\infty} \frac{z^{n}}{n!} \] Proszę szereg obciąć po \(100\) wyrazach i skorzystać z własnej implementacji podnoszenia do potęgi. Wynik proszę porównać z
N[Cos[1]]oraz
N[Sin[1]]Korzystając z funkcji
Solveproszę znaleźć współrzędne \((x , y)\) punktów na płaszczyźnie, które leżą na przecięciu
- prostej przechodzącej przez punkty \((-1 , 1)\), \((1 , 2)\)
- okręgu o środku w \((\frac{1}{2} , \frac{1}{2})\) i promieniu \(2\)
Dodatkowo proszę tą sytuację narysować (w Mathematica).
Proszę znaleźć wszystkie pierwiastki równania:
\[ z^{4} + z^{2} + 1 == 0 \]
oraz nanieść rozwiązania na płaszczyznę zespoloną (w Mathematice).
Proszę przygotować pakiet który dla danej funkcji \(f\) jednego argumentu rzeczywistego \(x\):
- rysuje jej wykres z zaznaczonymi, lokalnymi, minimami maksimami (na rysunku powinny pojawić się również współrzędne oraz informacja czy mamy do czynienia z minimum czy z maksimim)
- rysuje styczną do funkcji w zadanym miejscu
- liczy pole i zaznacza je na wykresie dla zadanego zakresu \(x\)
Zestaw 5
- zawartość “tablicy”
- włączyłem nagrywanie trochę późno więc krótkie nagranie z zajęć
- chaotyczny notebook z zajęć
- rysowanie fali
Proszę policzyć potencjał elektryczny \(U\) we wszystkich punktach \((i = 1 \ldots N , j = 1 \ldots N)\) kratownicy:
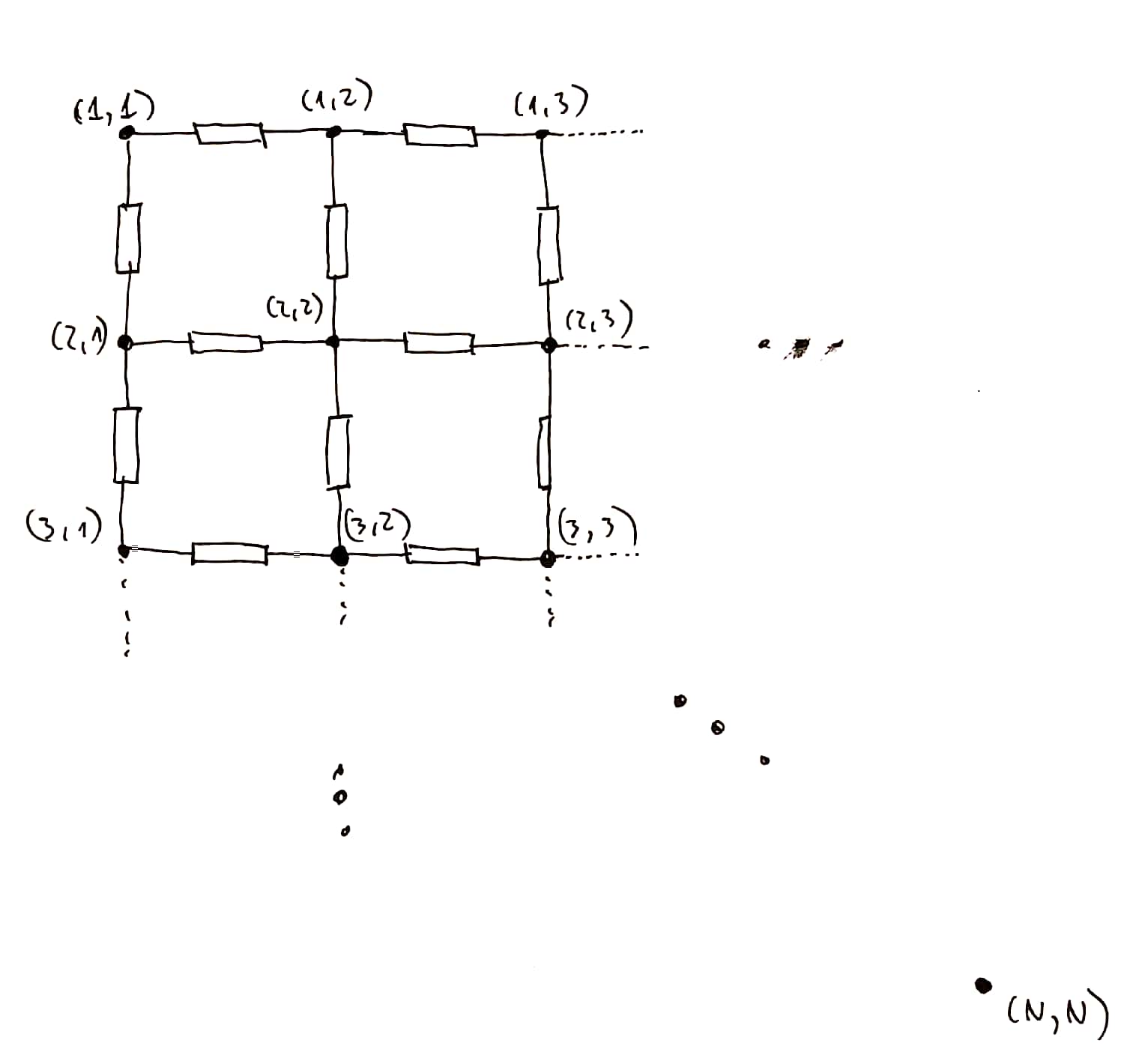
zakładająć:
- \(U_{(1 , 1)} = 0\),
- każdy opornik ma \(1 \Omega\)
- pomiędzy \((1 , 1)\) oraz \((N , N)\) przepływa prąd o natężeniu \(1 A\) (\(1 A\) wpływa do \((1,1)\) i wypływa z \((N , N)\))
- \(N\) przybiera różne wartości z zakresu \(2 \ldots 100\).
Można do tego podejść na wiele sposobów, ale chciałbym aby Państwo popracowali z macierzami dlatego proszę ułożyć odpowiedni układ równań macierzowych i rozwiązać go z wykorzystaniem:
LinearSolveWyniki proszę zwizualizować z wykorzystaniem
MatrixPlotKorzystając z wyników zadania A proszę wyznaczyć wartość zastępczą oporności takiego układu i zbadać jak zmienia się ona z \(N\).
Proszę rozwiązać problem Hanoi. Wszystkie kroki rozwiązania powinny być przedstawione w postaci animacji z wykorzystaniem:
Graphicsoraz:
ListAnimateMacierz:
\[ \left( \begin{array}{ccc} \frac{1}{3} & \frac{1}{3} \left(-1-\sqrt{3}\right) & \frac{1}{3} \left(1-\sqrt{3}\right) \\ \frac{1}{3} \left(\sqrt{3}-1\right) & \frac{1}{3} & \frac{1}{3} \left(-1-\sqrt{3}\right) \\ \frac{1}{3} \left(1+\sqrt{3}\right) & \frac{1}{3} \left(\sqrt{3}-1\right) & \frac{1}{3} \\ \end{array} \right) \]
obraca wektorem wokół pewnej osi. Proszę znaleźć tą oś.
Dana jest macierz \(N \times N\) \(A\), której elementy \(A_{i , j}\) przyjmują wartości równe \(0\) wszędzie oprócz:
- \(A_{i , i} = -\frac{2}{\Delta^{2}}\)
- \(A_{i , i - 1} = \frac{1}{\Delta^{2}}\)
- \(A_{i , i + 1} = \frac{1}{\Delta^{2}}\)
Przy czym
- kolumna o numerze \(N + 1\) jest utożsamiona z kolumną \(1\)
- kolumna o numerze \(0\) jest utożsamiona z kolumną \(N\)
- \(\Delta = \frac{1}{N}\)
- proszę rachunek przeprowadzić dla różnych wartości \(N\), na początek można przyjąć \(N = 100\)
Proszę policzyć wartości oraz wektory własne dla tej macierzy. Wektory własne dla wartości własnych o najmniejszej wartości bezwzględnej proszę narysować z wykorzystaniem
ListPloti zastanowić się jakie równanie reprezentuje ta macierz i co tak naprawdę zostało policzone.
Zestaw 6
- nagranie
- chaotyczne slajdy
- ocenzurowany (bez rozwiązania WH) notebook
- notebook z 17 XI 2022
Korzystając z funkcji:
Import[(*URL*) , "Data"]proszę ściągnąć z sieci (URL to adres) dane dotyczące wybranego procesu fizycznego. Następnie proszę te dane zwizualizować.
Opcja “Data” pozwala na importowanie ze stron internetowych tabel z danymi. Wynik działania funkcji trzeba będzie najprawdopodobniej przeszukać. Mogą być w tym pomocne:
PositionPart (*[[]]*)Proszę przygotować dwie funkcje liczące zbiór Mandelbrota. Jedna z wersji powinna korzystać z funkcji:
CompileProszę zmierzyć czas wykonywania programów z wykorzystaniem
TimingProszę zaimplementować własną wersję funkcji liczącej pochodną. W rachunkach proszę stosować symbole rozpoczynające się z małej litery (na przykład “sin” zamiast “Sin”) aby uniknąć konfliktu z wbudowanymi w Mathematicę definicjami.
Zestaw 7
Proszę zdefiniować typ danych opisujący płaszczyznę w przestrzeni trój wymiarowej
- płaszczyznę powinien określać zestaw (współrzędnych) trzech punktów do niej należących
- wzorzec definiujący ten typ danych powinien sprawdzać czy mamy do czynienia z trzema różnymi punktami
Mając ten typ danych proszę zaimplementować funkcję, która rysyje tą płaszczyznę. Wskazówka, proszę zajrzeć do dokumentacji:
InfinitePlaneoraz
Graphics2DKorzystając z typu danych zdefiniowanego w zadaniu A proszę napisać funkcję zwracającą wektor normalny do płaszczyzny. Dodatkowo proszę narysować kilka płaszczyzn oraz wykorzystująć:
Arrowkilka odpowiednich wektorów normalnych mających początek zaczeopiony w tych płaszczyznach.
Proszę zwrócić uwagę, że kolejnośc punktów w typie danych z A ma znaczenie.
Proszę zaimplementować funkcję, która biorąc jako argument typ danych z zadania A zwróci funkcję, która:
- pobiera dwie liczby rzeczywiste
- zwraca współrzędne punktu leżącego na płaszczyźnie.
Wzkazówka. Korzystając z funkcji
Orthogonalizeoraz
Normalizeproszę wprowadzić dwu wymiarowy układ współrzędnych na tej płaszczyźnie.
Proszę zaimplementować funkcję, która korzystając z typu danych w zadaniu A:
- pobierze dwie płaszczyzny
- zwróci funkcję pobierającą jedną liczbę rzeczywistą i zwracającą współrzędne punktu leżącego na przecięciu tych dwóch płaszczyzn
- proszę sprawdzić czy plaszczyzny nie są przypadkiem równoległe, jeżeli są proszę “rzucić” wyjątek wykorzystująć
ThrowProszę policzyć równanie ruchu dla paciorka o masie \(1\) nanizanego na poziomy pręt. Paciorek porusza się bez tarcia po pręcie i jest dodatkowo połączony ze ścianą sprężynką o stałej sprężystości \(1\). Rachunek proszę przeprowadzić korzystając z formalizmu Lagrangea w Mathematice. Następnie proszę rozwiązać otrzymane równanie ruchu korzystając z
NDSolvezakładając, że na początku ciało było w pozycji równowagi i miało prędkość początkową \(0.5\). Jednostki masy oraz odległości są dowolne.
Zestaw 8
Na te zajęcia nie ma nowych zadań. Będziemy mieli więcej czasu na indywidualne konsultacje oraz aby porozmawiac o projektach.
Zestaw 9
- notebook
- wystarczy uruchomić “Evaluate Notebook”
- macierz wymiarowości oraz twierdzenie Buckinghama
- momenty bezwładności
- youtube:
- notatki
- uwaga, w notatkach jest błąd 😊, czy potraficie go znaleźć
- nagrania nie będzie, bardzo przepraszam (nie nagrał się dźwięk, całe szczęście udało mi się rozwiązać ten problem i mam nadzieję, że następnym razem nie będzie już problemów)
Kolejne zastosowania macierzy…
Proszę napisać funkcję, która tworzy macierz wymiarowości. Funkcja powinna pobierać:
- listę jednostek bazowych (np
{t , m , l}oznaczające odpowiednio czas, masę oraz odległość) - listę wielkości fizycznych związanych z danym problemem (pojedyncza
wielkość może być np w reprezentacji korzystającej z potęg jednostek
bazowych
{-2 , 0 , 1}co można rozszyfrować jako \(t^{-2} m^{0} l^{1}\) czyli wymiar przyspieszenia)
Proszę sprawdzić działanie tej funkcji dla problemów:
- oscylacji wahadła matematycznego (interesujące wielkości fizyczne to: okres wahania, masa wahadła , długość wahadła , przyśpieszenie ziemskie)
- ochładzania cieczy z wykorzystaniem kostek lodu (interesujące wielkości fizyczne to: długość charakterystyczna dla kostek lodu, czas , temperatura, przewodnictwo cieplne, objętościowe ciepło właściwe)
oraz porównać z wikipedią.
Korzystając z wyników zadania A oraz funkcji
NullSpace proszę sprawdzić z jakich bezwymiarowych
wielkości można skonstruować prawa fizyczne rządzące obydwoma
problemami:
- oscylacji wahadła matematycznego (interesujące wielkości fizyczne to: okres wahania, masa wahadła , długość wahadła , przyśpieszenie ziemskie)
- ochładzania cieczy z wykorzystaniem kostek lodu (interesujące wielkości fizyczne to: długość charakterystyczna dla kostek lodu, czas , temperatura, przewodnictwo cieplne, objętościowe ciepło właściwe)
Proszę rozwiązać ponownie zadanie B ale tym razem z
wykorzystaniem wbudowanej w Mathemaitcę funkcji
DimensionalCombinations.
Rozważamy bryły sztywne na płaszczyźnie. Zakładamy, że płaskie bryły znajdują się w płaszczyźnie \(x\) - \(y\) oraz:
- \(-1 < x < 1\)
- \(-1 < y < 1\)
Proszę zaimplementować trzy funkcje zwracające:
- masę bryły
- środek masy bryły
- moment bezwładności bryły
Argumentem wszystkich tych trzech funkcji powinna być funkcja biorąca współrzędne na płaszczyźnie i zwracająca gęstość (powierzchniową) bryły.
Wyniki proszę porównać z wartościami tablicowymi
Wskazówka: można skorzystać z funkcji NIntegrate.
Proszę wykorzystać zadanie D oraz funkcję
DensityPlot do narysowania kilku figur oraz zaznaczenia ich
środków masy. W opisie wykresu powinna znaleźć się masa bryły oraz jej
moment bezwładności względem środka masy.
Zestaw 10
Korzystając z zadania D z zestawu 9 proszę przetestować twierdzenie Steinera. Aby to zrobić należy zdefiniować dwie identyczne bryły sztywne. Pierwsza jest umieszczona tak aby jej środek masy pokrywał się z początkiem układu współrzędnych. Druga jest przesunięta, powiedzmy w kierunku osi x, o \(\Delta\). Następnie można policzyć oraz porównać ich momenty bezwładności.
UWAGA: obydwie bryły powinny się mieścić w okienku zdefiniowanym w zadaniu D czyli \(-1 \lt x \lt 1\) oraz \(-1 \lt y \lt 1\).
Rozważamy sztywno względem siebie ułożone masy punktowe w trzech wymiarach:
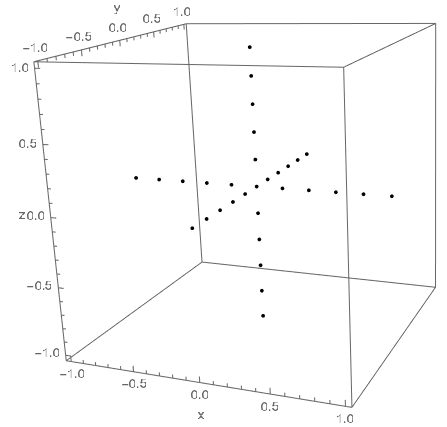
Każdy punkt o numerze \(i\) ma wapółrzędne \(r_{i}\), masę \(m_{i} = 1\) (dowolna jednostka masy), każde ramię krzyża ma długość \(2\) (dowolna jednosta odległości) a punkty są rozmieszczone co \(0.2\) (dowolna jednostka odległości).
Proszę w mathematice skonstruować taki system, narysować go oraz policzyc momenty mezwładności:
\[I_{xx} = \sum_{1 = 1}^{N} m_{i} (y_{i}^{2} + z_{i}^{2})\] \[I_{yy} = \sum_{1 = 1}^{N} m_{i} (x_{i}^{2} + z_{i}^{2})\] \[I_{zz} = \sum_{1 = 1}^{N} m_{i} (x_{i}^{2} + y_{i}^{2})\]
\[I_{xy} = \sum_{1 = 1}^{N} m_{i} (x_{i} y_{i})\] \[I_{xz} = \sum_{1 = 1}^{N} m_{i} (x_{i} z_{i})\] \[I_{yz} = \sum_{1 = 1}^{N} m_{i} (y_{i} z_{i})\]
Wskazówka: Można skorzystać z Riffle ,
Partition , Map , Union ,
Join oraz Table.
Proszę policzyć macierz momentów bezwładności dla systemu z zadania B:
\[ I_{CM} = \left( \begin{array}{ccc} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \\ \end{array} \right) \]
Tym razem proszę skorzystać z zależności:
\[ I_{CM} = \sum_{i = 1}^{N} -m_{i} \left[\widetilde{r_{i}}\right].\left[\widetilde{r_{i}}\right] \]
gdzie \(\left[\widetilde{x}\right]\) jest macierzą reprezentującą operator liczenia iloczynu skalarnego z \(x\). Proszę ten wynik porównać z zadaniem B.
Proszę przesunąć wszystkie punkty systemu z zadania B o \(1\) w kierunku \(x\). Następnie proszę policzyć, metodą z zadania C, macierz momentów bezwładności i porównać ją z macierzą liczoną z twierdzenia Steinera.
Zestaw 11
Na zajęciach chciałbym głównie porozmawiać z każdym z Państwa o projektach końcowych, kolokwium, zaliczeniach.
Proszę wyobrazić sobie wachadło fizyczne stworzone z wykorzystaniem
dowolnej, dwu wymiarowej bryły sztywnej z zadania D z
zestawu 9. Wachadło może się swobodnie obracać wokół “idealnego” (brak
tarcia oraz masy) zawiasu umieszczonego poza środkiem masy bryły.
Równania ruchu dla wachadła proszę rozwiązać z wykorzystaniem funkcji
NDSolve.
Wykorzystując zadanie A proszę tak dobrać warunki początkowe wachadła aby zademonstrować chaos w tym układzie.